According to game theory, free competition is not always ideal for society. Economists Gaëtan Fournier and Marco Scarsini use this perspective to study the spatial competition between several retailers. The retailers choose the location of their business to maximize their profits. According to the researchers’ model, pursuing an individual profit leads to stable but undesirable situations for the common good.
Why are hair salons always located on the same street? What is the point of putting all restaurants and cafés in the same area? Why is it, after countless hours on the road, you suddenly come across three gas stations all in the same place? Competition on price or quality is not the only type of competition that exists; there is also competition for space. Distance becomes a resource to be shared, whereas location becomes a cause for dispute.
Let’s say that several ice cream vendors are to be set up on a beach. Where would each vendor place their stand? We can assume that customers would choose one vendor over another as a result of the vendor’s proximity to their placement. However, the vendor’s choice is made in a situation of uncertainty, since they do not know where the other vendors will be set up. So, how can this conundrum be solved? In economics, game theory models such situations, where each economic agent does not know the choice of others in advance.
Stability in Anarchy
The authors of the study used this theory to look at spatial competition between retailers. They sought to find out whether there is a solution which allows competition for place to be stabilized in the long term. To do this, they made a model of a network—similar to a city map—and had retailers choose the location of their store from amongst the many streets. Consumers walk through all the streets equally, and the retailers are in competition with each other. The more customers each retailer has, they more profit they make. Consumers, on the other hand, buy from the nearest retailer. The researchers do not consider competition on price or quality in their model, purely geographical position. They deem that prices and products are imposed upon the retailer, such as corporate franchises or pharmacies.

2This allows the researchers to determine whether a situation exists where the retailers are satisfied and no longer look to move. This equilibrium situation, known as Nash equilibrium in game theory, is stable in the long term because none of the retailers would, after considering their competitors’ choices, decide to deviate from their selected spot.
We might think that the free competition represented on this city map would lead to a level of instability (caused by the retailers’ constant fight for a better place) that would prevent the situations from lasting. However, the researchers' model shows that an equilibrium is established if the number of retailers is indeed large enough.1 The retailers’ location on the network at this equilibrium can then be mapped and determined permanent. The researchers have thus characterized this “Nash equilibrium.” We know this equilibrium is stable since none of the retailers would move from their position independently from the others—they’d otherwise lose out!
- 2Of course, the model is not always corroborated in real situations, since it does not take into account all the parameters of reality. The concept of the Nash equilibrium also fails to consider the fact that retailers can move all at the same time or come to a collective solution. However, the model does reveal certain economic mechanisms and raises useful questions for society.
- 1The number of retailers needed to form a Nash equilibrium depends on the structure of the city (number and length of streets, etc.).
“The Price of Anarchy”
It should be noted that, while the Nash equilibrium considers retailers’ choice, it nevertheless fails to consider consumer well-being. Consumer well-being in this case is the average distance one travels to buy a good. Ideally, the average is as low as possible and allows consumers to travel as little as possible. This situation, known as the social optimum, is the most beneficial for consumer but is not a Nash equilibrium, since it is unstable. In order for the social optimum to exist, it must be protected by a city planner. In this case, for example, a planner would distribute retailers as evenly as possible around the network to ensure that the distance traveled by consumers remains as short as possible.
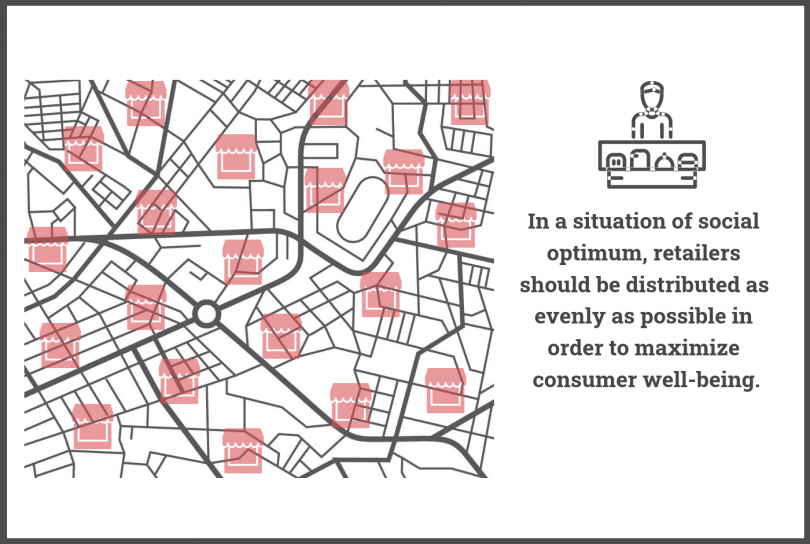
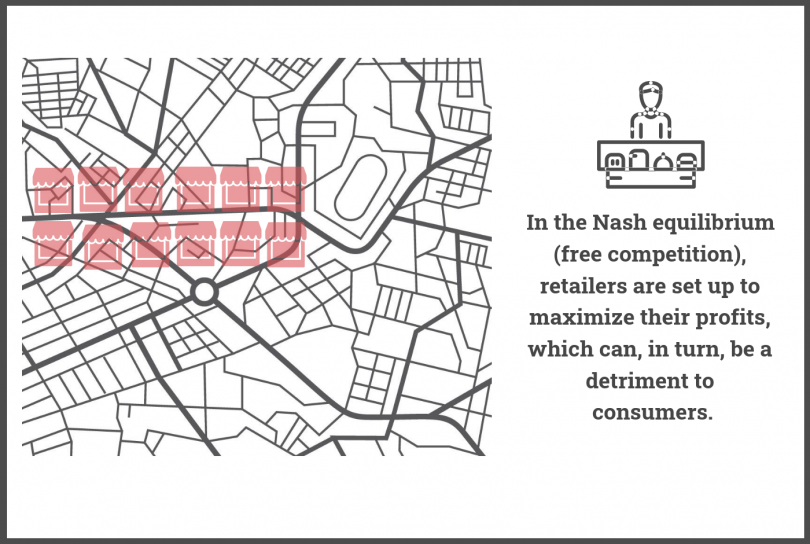
And in order to determine whether the planner must force retailers to respect the social optimum, they need to know the “Price of Anarchy.” The Price of Anarchy here is the ratio that compares the distance traveled by consumers in the optimal situation with the worst Nash equilibrium.
There is, it turns out, not a single situation of equilibrium. The choice made by retailers in free competition can lead to several different scenarios. The distribution of the retailers on the map could, for example, be quite different.
So, what tips the balance in favor of one or the other of the equilibrium scenarios? One discipline in economics, known as evolutionary game theory, is particularly interested in this question. This theory seeks to find out how the dynamics of a particular situation have been influenced to shift towards one equilibrium over another. However, the researchers in this study were not looking to predict a particular equilibrium. They have instead considered the retailers to be self-seeking agents and have determined that the worst-case scenario happens by bad luck. And, through this, they evaluate the Price of Anarchy.
Here, the cost between the two is doubled, so consumers must travel twice as far in the equilibrium situation than they’d be required in the optimum. This shows how wide the gap is between worst-case scenarios of free competition and ideal situations. It furthermore highlights how the selfish pursuit of profit does not necessarily lead to the common good. So, while collaboration or the pursuit of collective well-being could reduce the consumer's social cost, free competition does not, in contrast, always lead to a social ideal.














